NUMERICAL SIMULATION AND ANALYSIS OF A CAPUTO FRACTIONAL-ORDER SEIR MODEL FOR COVID-19 PREVALENCE USING THE HERMITE POLYNOMIAL COLLOCATION AND LAPLACE-ADOMIAN DECOMPOSITION METHODS

Authors

  • Morufu Oyedunsi Olayiwola
    Osun State University
  • Ajimot Folasade Adebisi
    Osun State University
  • Bosede Abubakre
    University of Ilesa
  • Akeem Olarewaju Yunus
    Osun State University

Keywords:

Hermite Polynomials, Collocation Methods, Simulations Analysis, Laplace-Adomian Decomposition Method, SARS-CoV-2 Variants

Abstract

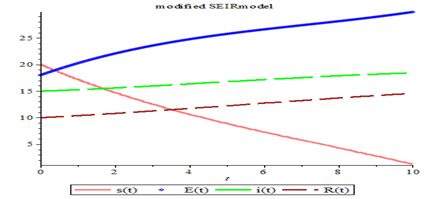
COVID-19 poses major public health challenges due to its high transmissibility. This study presents a novel numerical framework based on a fractional-order SEIR model to explore serotonin transfer and evaluate control strategies for emerging SARS-CoV-2 variants. By including the exposed compartment, the extended SEIR model offers improved insight into variant transmission dynamics. Two advanced numerical techniques are compared: the Hermite Collocation Method (HCM) and the Laplace-Adomian Decomposition Method (LADM). Due to the model's inherent nonlinearity, finding exact solutions is difficult. To overcome this, the model is transformed into a nonlinear algebraic system using Hermite polynomial collocation with Caputo fractional derivatives. Expansion coefficients representing the approximate solution are computed with Maple software, enabling precise analysis of disease dynamics. The fractional derivative framework captures memory effects that influence transmission, particularly under changing viral conditions. Simulations reveal that both methods effectively reduce transmission and hospitalizations, but HCM outperforms LADM in accuracy and convergence speed. The results demonstrate the strength of fractional-order modeling in describing real-world epidemic patterns, especially with evolving COVID-19 variants. HCM’s high reliability positions it as a valuable predictive tool for health authorities. Its precision allows for early detection of outbreaks and supports the formulation of responsive public health strategies. This study emphasizes the importance of advanced mathematical modeling in managing infectious diseases and recommends HCM as a reliable method for anticipating variant behavior. Policymakers can apply this approach to develop timely, adaptive interventions for future COVID-19 variants and similar pandemics.

Dimensions

Abdullah, M., Yaseen, M., & De la Sen, M. (2022). An efficient collocation method based on Hermite formula and cubic B-splines for numerical solution of the Burgers’ equation. Mathematics and Computers in Simulation, 197, 166–184. Elsevier.

Adebisi, A. F., Olayiwola, M. O., Adediran, I. A., &Alaje, A. I. (2024). A novel mathematical model and homotopy perturbation method analyzing the effects of saturated incidence and treatment rate on COVID-19 eradication. Iranian Journal of Science, 48(3), 625–636.

Adebisi, A. F., Uwaheren, O. A., Abolarin, O. E., Raji, M. T., Adedeji, J. A., & Peter, O. J. (2021). Solution of typhoid fever model by Adomian decomposition method. Journal of Mathematics and Computer Science, 11(2), 1242–1255.

Adewale Adedokun, K., OyedunsiOlayiwola, M., AdedapoAlaje, I., OlarewajuYunus, A., OlalekanOladapo, A., &Oyeleye Kareem, K. (2024). A Caputo fractional-order model of tuberculosis incorporating enlightenment and therapy using the Laplace–Adomian decomposition method. International Journal of Modelling and Simulation, 1–15. Taylor & Francis.

Aboiyar, T., &Enonche, F. Probabilists' Hermite Collocation Method for solving two point higher order linear boundary problems of ordinary differential equations. [Publisher not specified].

Ahmed, S., Jahan, S., Shah, K., &Abdeljawad, T. (2024). On mathematical modelling of measles disease via collocation approach. AIMS Public Health, 11(2), 628. AIMS Press.

Alaje, A. I., &Olayiwola, M. O. (2023). A fractional-order mathematical model for examining the spatiotemporal spread of COVID-19 in the presence of vaccine distribution. Healthcare Analytics, 4, 100230. https://doi.org/10.1016/j.health.2023.100230. Elsevier.

Anietie, E. U., &Ini-Obong, E. (2022). SEIR model with a vaccination parameter using COVID-19 as a case study. The Journals of the Nigerian Association of Mathematical Physics, 63, 135–142.

Apostolopoulos, V., Feehan, J., &Chavda, V. P. (2024). How do we change our approach to COVID with the changing face of disease? Expert Review of Anti-infective Therapy, 22(5), 279–287. Taylor & Francis.

Asimiyu, O. O., Yunus, A. O., Omoloye, M. A., &Olayiwola, M. O. (2025). Novel approaches to malaria control and eradication using fractional-order modeling and numerical simulations. Next Research, 100205.

Aydin, S. (2018). The foundational SIR model: Dividing the population into susceptible, infected, and recovered compartments. Journal of Epidemiological Studies, 10(2), 45–60.

Erdem, K., &Yalçınbaş, S. (2012). Bernoulli polynomial approach to high-order linear differential-difference equations. AIP Conference Proceedings, 1479, 360–364. https://doi.org/10.1063/1.4756138

Gheisari, F. (2024). Navigating the future of COVID-19 outbreaks: Trends, challenges, and strategies in 2024. Journal of Clinical Case Studies, Reviews & Reports, 2(3), 1–16.

Gülsu, M., Yalman, H., Öztürk, Y., &Sezer, M. (2011). A new Hermite Collocation Method for solving differential-difference equations. Applied and Applied Mathematics, 6, 1856–1869.

Henka, Y., Lemita, S., &Aissaoui, M. Z. (2023). Hermite wavelets collocation method for solving a Fredholmintegro-differential equation with fractional Caputo–Fabrizio derivative. Proyecciones (Antofagasta), 42(4), 917–930.

Hussain, R., Ali, A., Chaudary, A., Jarral, F., Yasmeen, T., &Chaudary, F. (2017). Numerical solution for mathematical model of Ebola virus. International Journal of Advanced Research, 5, 1532–1538.

Jacob, E., Olumi, T., Ibrahim, A., & Suberu, I. (2022). Numerical simulation of coronavirus disease epidemic based on established susceptible-exposed-infectious-recovered-undetectable-susceptible model. Fudma journal of sciences, 6(5), 224-230. https://doi.org/10.33003/fjs-2022-0605-1731

Manohara, G., &Kumbinarasaiah, S. (2024). Numerical approximation of fractional SEIR epidemic model of measles and smoking model by using Fibonacci wavelets operational matrix approach. Mathematics and Computers in Simulation, 221, 358–396. Elsevier.

Mbainguesse, D., Seid, A. M., Abbo, B., &Paré, Y. (2024). Hermite operational matrix and collocation methods for solving linear fractional Fredholmintegro-differential equation. Far East Journal of Applied Mathematics, 117(1), 1–18.

Moreno Martín, S., RosGiralt, L., & Celaya Llover, E. (2022). Collocation methods for second order systems. In Proceedings of the XVIII Robotics: Science and Systems Conference (RSS) (pp. 1–11).

Nwokoye, C. H., Mbeledogu, N. N., Paul, R. U., &Ugwunna, C. (2022, October). Complementing malware epidemic agent-based models with routing protocols of communication networks using NetLogo. In International Conference on Information and Communication Technology for Competitive Strategies (pp. 833–847). Springer Nature Singapore.

Olayiwola, M. O., &Alaje, A. I. (2024). Mathematical modelling of diphtheria transmission and vaccine efficacy using Nigeria. Modeling Earth Systems and Environment, 10(3), 3941–3967. Springer.

Olayiwola, M. O., &Yunus, A. O. (2024). Mathematical analysis of a within-host dengue virus dynamics model with adaptive immunity using Caputo fractional-order derivatives. Journal of Umm Al-Qura University for Applied Sciences, 1–20.

Olayiwola, M. O., Alaje, A. I., &Yunus, A. O. (2024a). Modelling the impact of education and memory on the management of diabetes mellitus using Atangana–Baleanu–Caputo fractional order model. Nonlinear Dynamics, 1–21. Springer.

Olayiwola, M. O., Alaje, A. I., &Yunus, A. O. (2024b). A Caputo fractional order financial mathematical model analyzing the impact of an adaptive minimum interest rate and maximum investment demand. Results in Control and Optimization, 14, 100349. Elsevier.

Olayiwola, M. O., Adebisi, A. F., & Abubakre, B. (2025). Mathematical modeling of a nonlinear SEIR model of COVID-19 via the numerical solution of Hermite collocation method. Nonlinear Science, 100048.

Pirim, A. N., &Ayaz, F. (2016). A new technique for solving fractional order systems: Hermite Collocation Method. Springer Physics Mathematics and Statistics, 7, 2307. Springer.

Srinivasa, K., Baskonus, H. M., & Guerrero Sánchez, Y. (2021). Numerical solutions of the mathematical models on the digestive system and COVID-19 pandemic by Hermite wavelet technique. Symmetry, 13(12), 2428. MDPI.

Yadav, R. S. (2020). Mathematical modeling and simulation of SIR model for COVID-2019 epidemic outbreak: A case study of India. medRxiv, 2020–05. https://doi.org/10.1101/2020.05.20.20108308

Yunus, A. O., &Olayiwola, M. O. (2024a). The analysis of a novel COVID-19 model with the fractional-order incorporating the impact of the vaccination campaign in Nigeria via the Laplace–Adomian Decomposition Method. Journal of the Nigerian Society of Physical Sciences, 1830–1830.

Yunus, A. O., &Olayiwola, M. O. (2024b). Mathematical modeling of malaria epidemic dynamics with enlightenment and therapy intervention using the Laplace–Adomian decomposition method and Caputo fractional order. Franklin Open, 100147. Elsevier.

Yunus, A. O., &Olayiwola, M. O. (2025). Dynamics of Ebola virus transmission with vaccination control using Caputo–Fabrizio fractional-order derivative analysis. Modeling Earth Systems and Environment, 11(3), 1–18. Springer.

Yunus, A. O., Olayiwola, M. O., Adedokun, K. A., Adedeji, J. A., &Alaje, I. A. (2022). Mathematical analysis of fractional-order Caputo’s derivative of coronavirus disease model via Laplace Adomian decomposition method. Beni-Suef University Journal of Basic and Applied Sciences. https://doi.org/10.1186/s43088-022-00326-9 . Springer.

Yunus, A. O., Olayiwola, M. O., Omoloye, M. A., &Oladapo, A. O. (2023). A fractional order model of Lassa disease using the Laplace–Adomian Decomposition Method. Health Analytics Journal. http://doi.org/10.1016/j.health.2023.10.100167. Elsevier.

Yüzbaşı, Ş., &Yıldırım, G. (2023). A Pell–Lucas collocation approach for an SIR model on the spread of the novel coronavirus (SARS CoV-2) pandemic: The case of Turkey. Mathematics, 11(3), 697. MDPI.

Published

11-10-2025

How to Cite

Olayiwola, M. O., Adebisi, A. F., Abubakre, B., & Yunus, A. O. (2025). NUMERICAL SIMULATION AND ANALYSIS OF A CAPUTO FRACTIONAL-ORDER SEIR MODEL FOR COVID-19 PREVALENCE USING THE HERMITE POLYNOMIAL COLLOCATION AND LAPLACE-ADOMIAN DECOMPOSITION METHODS. FUDMA JOURNAL OF SCIENCES, 9(10), 296-311. https://doi.org/10.33003/fjs-2025-0910-3837

Issue

Vol. 9 No. 10 (2025): FUDMA Journal of Sciences - Vol. 9 No. 10

Section

Research Articles
Copyright & Licensing

Copyright (c) 2025 Morufu Oyedunsi Olayiwola, Ajimot Folasade Adebisi, Bosede Abubakre, Akeem Olarewaju Yunus

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Olayiwola, M. O., Adebisi, A. F., Abubakre, B., & Yunus, A. O. (2025). NUMERICAL SIMULATION AND ANALYSIS OF A CAPUTO FRACTIONAL-ORDER SEIR MODEL FOR COVID-19 PREVALENCE USING THE HERMITE POLYNOMIAL COLLOCATION AND LAPLACE-ADOMIAN DECOMPOSITION METHODS. FUDMA JOURNAL OF SCIENCES, 9(10), 296-311. https://doi.org/10.33003/fjs-2025-0910-3837

Most read articles by the same author(s)